Quadratic Gaussian Splatting

1. 信息

文章：Quadratic Gaussian Splatting for Efficient and Detailed Surface Reconstruction
代码：QuadraticGS/QGS: The official implementation for the paper “Quadratic Gaussian Splatting for Efficient and Detailed Surface Reconstruction.”

2. 一些知识

1. 二次型与标准对角化、几何意义

首先，假设有 $n$ 个变量 $x_i$ 构成一个多项式，其中每一项最高次幂为 2，可以表示如下

$f(x_1,x_2,...,x_n)=a_{1,1}x_1^2+2a_{1,2}x_1x_2+...+a_{n,n}x_n^2$

这是二次型的标准形式，同样的，如果二次型多项式中 只有某变量的平方项，则称为二次型的标准型，即：

$f(x_1,x_2,...,x_n)=a_{1,1}x_1^2+a_{2,2}x_2^2+...+a_{n,n}x_n^2$

以矩阵形式表达，可以写作：

$\begin{align*} f(x_1,x_2,...,x_n) &= \left [ \begin{matrix} x_1 &x_2 &... &x_n \end{matrix} \right ] \left [ \begin{matrix} a_{1,1} &a_{1,2} &... &a_{1,n}\\ a_{2,1} &a_{2,2} &... &a_{2,n}\\ ...\\ a_{n,1} &a_{n,2} &... &a_{n,n} \end{matrix} \right ] \left [ \begin{matrix} x_1\\ x_2\\ ...\\ x_n \end{matrix} \right ]\\ &=\mathbf{X}^T\mathbf{A}\mathbf{X} \end{align*}$

由于二次型实际上是二次多项式，而由于 $(a+b)^2$ 的性质，二次型矩阵 $\mathbf{A}$ 有性质 $a{i, j}=a{j, i}$ ，所以 $\mathbf{A}$ 是对称矩阵。

由于在实际应用中，大多关注项在实数范围内的矩阵，所以以下的理论均在实数范围内的二次型（Real quadratic forms）中。
对于每一个二次型矩阵，由于其本身是对称矩阵，所以它们一定能够对角化，即化简为：

$\begin{align*} &\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{-1}\\ &\mathbf{Q}是正交矩阵,即列向量之间正交,\mathbf{Q}^{-1}=\mathbf{Q}^{T}\\ &\mathbf{\Lambda}是对角矩阵 \end{align*}$

并且在 Sylvester’s law of inertia - Wikipedia 中有以下定理，如果基的变换（即 $\mathbf{A}\rightarrow \mathbf{\Lambda}$）是由可逆矩阵带来的 ($\mathbf{Q}$ 是可逆的)，则 $\mathbf{\Lambda}$ 中对角线上的值只能是 0,-1,1。且元组 $(n0,n{+},n_{-})$ 仅由 $A$ 决定，而不受变换矩阵的控制，其中 $n_0$ 代表对角线上为 0 的个数，其余同理。
根据对角线上值的特性，可将矩阵分为以下四类：

$\lambda_i>0$ 对每个特征值（对角线上的值）均成立，该矩阵为正定矩阵
$\lambda_i<0$ 对每个特征值均成立，该矩阵为负定矩阵
$\lambda_i$ 均不为 0，为非退化矩阵
$\lambda_i$ 存在大于 0 或小于 0，为各向同性矩阵

在标准对角化之后，对角矩阵 $\mathbf{\Lambda}$ 的特征值可以反映二次型所表示的几何形状

所以特征值非 0
- 如果特征值均为正，为椭球面
- 如果特征值为负，为虚椭球面（半径是虚数）
- 如果一些特征值是正数，一些是负数，则是双曲面
存在一个或多个特征值为 0
- 为抛物面
  3. 简要介绍
  quadratic Gaussian splatting，即 QGS，是一种利用二次曲面作为重建单位的高斯重建方法，其想法受 2DGS 指导，2DGS 中的圆盘重建为多视角一致性提供了良好的基础，但 2DGS 中将圆盘作为重建单位也导致了重建结果过于平滑，损失了物体本身的细节，QGS 在 2DGS 的基础之上，将圆盘变形为可以“凸起，凹陷”的圆盘，即抛物面，达到更好的表面重建结果。

4. 技术细节

1. 高斯重建

3dgs 的公式如下

$\begin{align*} &G(x)=exp(-\frac{1}{2}(\mathbf{x}-\mathbf{p}_k)^T\sum\nolimits^{-1}(\mathbf{x}-\mathbf{p}_k))\\ &\sum\nolimits=\mathbf{R}\mathbf{S}\mathbf{R}^T\mathbf{S}^T\\ &\sum\nolimits^{'}=\mathbf{J}\mathbf{W}\sum\nolimits\mathbf{J}^T\mathbf{W}^T\\ &C(\mathbf{p})=\sum\limits_{i=0}^{N-1}G_{i}^{2D}(\mathbf{p})\alpha_ic_i\prod_{j=0}^{i-1}(1-G_{j}^{2D}(\mathbf{p})) \end{align*}$

以上便是常规 3dgs 的高斯函数表示，和从世界坐标系-屏幕坐标系-图形坐标系的的转换，以及最后使用 alpha-blending 对渲染图像上某个像素的颜色渲染公式。
对于 3dgs 和其变体 2dgs，它们使用的体素单位都是高斯，QGS 也是，但是三者形态各有不同，即：

3dgs：椭球
2dgs：平面圆盘
QGS：二次曲面（抛物面）

高斯形态类型

而在 QGS 的作者论述中，对于多孔且棱角分明的场景重建，3gds 会造成拟合不到平面的问题，而 2dgs 在表面曲率较大的时刻难以拟合平面，比如孔洞这种位置，会造成直接过于平滑的重建效果，qgs 则能避免以上两种问题，如图：

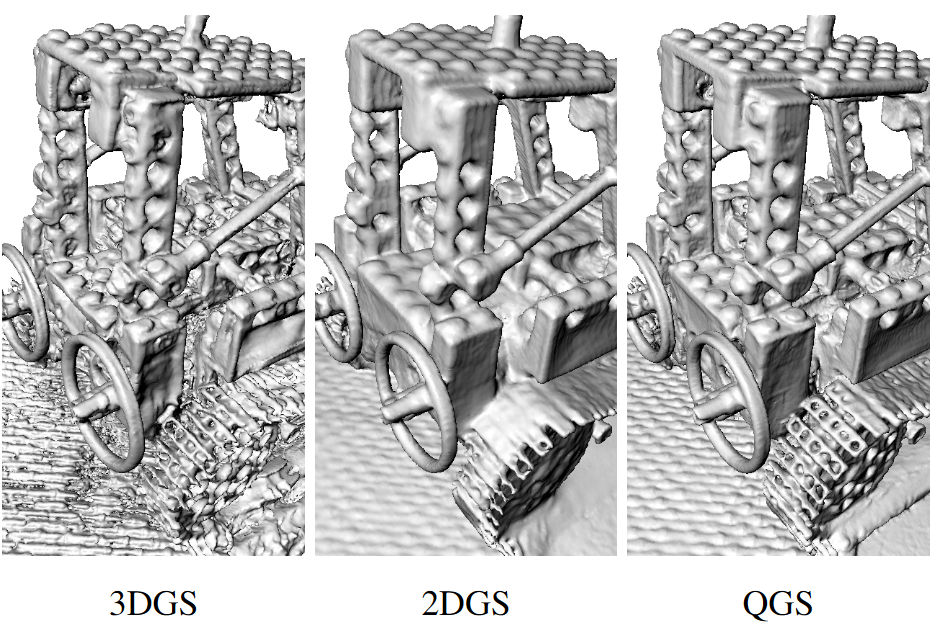
前述方法对比

2. 二次曲面

上节中提到 QGS 使用的是二次曲面，而在齐次坐标系下，二次曲面常常是隐式定义的，即

$\begin{align*} &\mathbf{x}=[x,y,z,1]\in R^4\\ &f(x,y,z)=\mathbf{x}^T\mathbf{Q}\mathbf{x}=0 \end{align*}$

$\mathbf{Q}\in R^4$ ，是一个四阶矩阵，即二次型矩阵，但由于其本身矩阵的基性质不够好，不能直接反应二次曲面的特征向量和缩放系数，即 3dgs 那样的 $\sum\nolimits=\mathbf{R}\mathbf{S}\mathbf{R}^T\mathbf{S}^T$ 性质，所以通过求出合同矩阵 $D$ ，即替换矩阵的基，能够将矩阵等价转换为性质更好的矩阵，即

$\begin{align*} &\mathbf{Q}=\mathbf{T}^{-T}\mathbf{D}\mathbf{T}^{-1} \end{align*}$

具体过程为

$\begin{align*} f&=\mathbf{x}^T\mathbf{Q}\mathbf{x}\\ &=\mathbf{y}^T(\mathbf{T}^T\mathbf{Q}\mathbf{T})\mathbf{y}\\ &=\mathbf{y}^T\mathbf{\Lambda}\mathbf{y}\\ \end{align*}$

即对二次型矩阵的标准型计算过程，其中对角化中产生的 $\mathbf{T}$ 的前三行和前三列的子矩阵，可以被分解为 $\mathbf{RS}$ ，即二次曲面的方向向量矩阵和系数向量的乘积，且 $\mathbf{T}$ 的第四列代表了二次曲面的位置，对角化后的标准型矩阵，仅在对角线上有元素，且取值只存在 -1,0,1 三种情况，而这三种取值则反应了二次曲面的形状，是椭球体，还是平面等。具体参考 2.1 节

$\begin{align*} &\mathbf{T}= \left [ \begin{matrix} \mathbf{u} &\mathbf{v} &\mathbf{w} &\mathbf{c} \\ 0 &0 &0 &1 \end{matrix} \right ]\\ &[\mathbf{u}\ \mathbf{v}\ \mathbf{w}]=\mathbf{RS}\\ &\mathbf{R}=[\mathbf{r}_1\ \mathbf{r}_2\ \mathbf{r}_3]\\ &\mathbf{S}=diag(s_1,s_2,s_3) \end{align*}$

得到良好的形式之后，就需要定义二次曲面上任意一点的高斯函数值了，但在这之前，先需要定义高斯函数的均值和方差，才能描述其上一点的高斯函数值。

3. 测地线距离

作者认为，二次曲面上点之间的值，应被描述为沿曲面行进的距离，这样可以达到将高斯的能量集中于表面，同时，数学上有此种定义。

测地线定义

但作者提及，某些二次曲面的性质不够好，会导致测地距离没有解析解，只能通过数值方法进行计算，所以他只选择二次曲面中的抛物面作为体素单元。
具体来说，将上文中的二次曲面函数进行进一步转换，得到

$\begin{align*} f(x,y,z) &=\mathbf{x}^T \left [ \begin{matrix} \mathbf{R} &\mathbf{c}\\ 0 &1 \end{matrix} \right ] \overline{D} \left [ \begin{matrix} \mathbf{R} &\mathbf{c}\\ 0 &1 \end{matrix} \right ] \mathbf{x}\\ &=\mathbf{\hat{x}}^T \left [ \begin{matrix} \frac{d_{11}}{s_1^2} &0 &0 &0\\ 0 &\frac{d_{22}}{s_2^2} &0 &0\\ 0 &0 &0 &-\frac{d_{33}}{2s_3}\\ 0 &0 &\frac{d_{33}}{2s_3} &0\\ \end{matrix} \right ] \mathbf{\hat{x}}\\ &=\frac{d_{11}}{s_1^2}\hat{x}^2+\frac{d_{22}}{s_2^2}\hat{y}^2-\frac{d_{33}}{s_3^2}\hat{z}\\ &=0 \end{align*}$

由于 $d_{ii}$ 的取值代表了抛物面的形状，如椭球体、平面，但它的取值是离散的，导致函数本身不可微，所以需要进行一些变换，作者在此用缩放比例的函数进行替代，使二次型函数变的可微

$\begin{align*} &f(\hat{x},\hat{y},\hat{z})=\frac{sign(s_1)}{s_1^2}\hat{x}^2+\frac{sign(s_2)}{s_2^2}\hat{y}^2-\frac{1}{s_3}\hat{z}=0\\ &sign(s,t)=tanh(t)exp(x) \end{align*}$

同时将其转换为显式形式，便于表达，即

$\hat{z}(\hat{x},\hat{y})=s_3(\frac{sign(s_1)}{s_1^2}\hat{x}^2+\frac{sign(s_2)}{s_2^2}\hat{y}^2)$

再转换为柱坐标系下的表示，即由 $\theta, \rho, z$ 组成的坐标系，即

$\begin{align*} \hat{z}(\theta,\rho)&=s_3(\frac{sign(s_1)\cos\theta^2}{s_1^2}+\frac{sign(s_2)\sin\theta^2}{s_2^2})\rho^2\\ &=a(\theta)\rho^2\\ &\hat{x}=\rho\cos\theta\\ &\hat{y}=\rho\sin\theta \end{align*}$

转换为柱坐标系的原因，主要是利于测地距离的计算，即高斯函数中均值的计算，这是由于，在柱坐标系下，取一个平面 $\theta=\theta_0, \rho\in (0,\rho_0)$ ，它与抛物面相交的曲线的长度，正好是抛物面原点到点 $\hat{\mathbf{p}}=(\rho_0, \theta_0, \hat{z}(\theta_0, \rho_0))$ 的测地线距离，并且形式非常好。
曲线 $\mathbf{r}(t)=[x(t),y(t),z(t)]^T$ 的弧长计算公式为

$L=\int_a^b||\mathbf{r}'(t)||dt$

而在柱坐标系中，变量即为 $\rho$ ，所以曲线的弧长计算公式为

$\begin{align*} l(a,\rho_0) &=\int_{0}^{\rho_0}\sqrt{\sin\theta^2+\cos\theta^2+(2at)^2}dt\\ &=\int_0^{\rho_0}\sqrt{1+(2at)^2}dt\\ &=\frac{\ln(\sqrt{u^2+1}+u)+u\sqrt{u^2+1}}{4a}\\ &where\ u=2a\rho_0\\ &\frac{dx}{dt}=\cos\theta\\ &\frac{dy}{dt}=\sin\theta\\ &\frac{dz}{dt}=2a(\theta)t\\ \end{align*}$

所以柱坐标系的作用是，将曲线弧长（即测地线距离）的计算形式变的更简洁。

4. 方差

由于二维高斯分布，外形如椭圆，其中，椭圆的两轴即为 $(s_1, s_2)$ 两个缩放系数，而椭圆上一点的表示在极坐标系下可以表示为 $(\theta_0,\rho_0)$ ，对应的 $\theta_0$ 的标准差就是 $\rho_0$ 。

所以二次曲面上每一点的高斯函数，以二次曲面原点为均值 $\mu$，所以 $x-\mu$ 为测地距离，方差为二维高斯分布中标准差的平方，即

$\begin{align*} &G(\hat{\mathbf{p}}(\theta_0,\rho_0))=exp(-\frac{l(a(\theta_0),\rho_0)^2}{2\sigma(\theta_0)^2})\\ &\sigma(\theta_0)=\rho_0 \end{align*}$

得到二次曲面高斯函数表达方式后，可以对其中的一些变量进行变动，查看其与平面高斯的高斯函数之间的关联。将二次曲面的 $s_3$ 趋近于 0，这会导致测地距离计算公式中的 $a$ 趋于 0，进而导致测地距离趋近于 L2 即欧几里得距离，所以说，二次曲面高斯是更一般化的二维高斯，2DGS 同样也是 QGS 的一种特殊情况了。但 QGS 含有曲面特征，相对于 2DGS，其对表面重建的能力更强。

5. 光线求交

由于二次曲面的特性，导致与曲面相交的光线会产生 2 个交点，即 $\hat{\mathbf{p}}_n$ 和 $\hat{\mathbf{p}}_f$ ，即

$\begin{align*} &\hat{\mathbf{p}}=\hat{\mathbf{o}}+t\hat{\mathbf{d}}\\ &\hat{\mathbf{p}},\hat{\mathbf{t}},\hat{\mathbf{o}}\in R^3 \end{align*}$

设相机中心为 $\hat{\mathbf{o}}=[\hat{o}^1,\hat{o}^2,\hat{o}^3]^T$，和光线方向 $\hat{\mathbf{r}}=[\hat{r}^1,\hat{r}^2,\hat{r}^3]^T$，所以光线上任意一点可以表示为

$\mathbf{x}= \left [ \begin{matrix} \hat{o}^1+t\hat{r}^1 \\ \hat{o}^2+t\hat{r}^2 \\ \hat{o}^3+t\hat{r}^3 \\ \end{matrix} \right ]$

带入二次曲线的隐式表达，即

$\begin{align*} &f(\hat{x},\hat{y},\hat{z})=\frac{sign(s_1)}{s_1^2}\hat{x}^2+\frac{sign(s_2)}{s_2^2}\hat{y}^2-\frac{1}{s_3}\hat{z}=0\\ &sign(s,t)=tanh(t)exp(x) \end{align*}$

由于在方程中，只有深度 $t$ 是未知数，所以结果为一个以 $t$ 为未知数的一元二次方程，即

$\begin{align*} &At^2+Bt+C=0\\ &t_n=\frac{-B-sign{(A)}\sqrt{B^2-4AC}}{2A}\\ &t_f=\frac{-B+sign{(A)}\sqrt{B^2-4AC}}{2A} \end{align*}$

而根据高斯能量分布和远近的关系，和多视角一致性的原则，作者制定了以下的交点选择方式

近点的测地线距离小于 $3\sigma (\theta_n)$ ，选择近点
远点的测地线距离小于 $3\sigma (\theta_f)$ ，选择远点
否则，光线与曲面无交点。

6. 法线和曲率

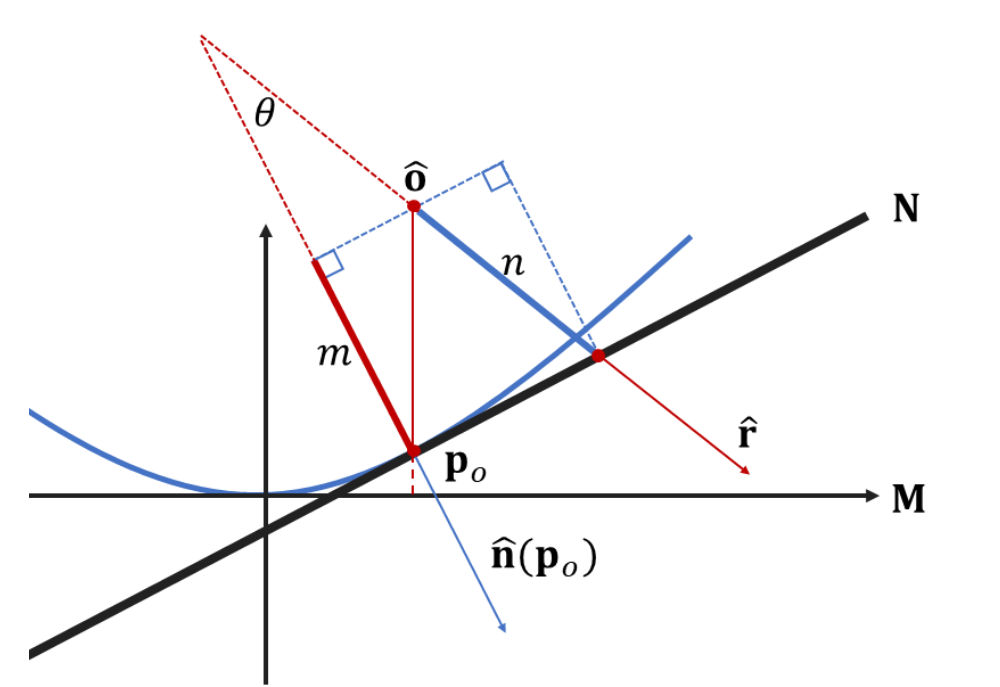
法线和深度示意图

对于以上求解的近点和远点的深度距离，在大部分情况下是可用的，但在二次曲面近似于平面，即上述解的 $A$ 过小时，会给回传带来浮点下溢等问题，所以作者在这里认为，当 $A<1e-6$ 时，抛去方程中的 $At^2$ ，直接将 $t=-\frac{C}{B}$ 作为解。在几何意义上，该解代表 光线与摄像机做出一条垂线与二次曲面相交点处的切平面的交点之间的距离，即上图的 $n$ 。
下面是作者对该解析解 $t=-\frac{C}{B}$ 的推导。
对于二次曲面，作者 3计算法线的方式如下所示，通过将二次曲面的前两个特征向量进行叉乘得到垂直于二次曲面的面 $\mathbf{M}$ ，做相机原点与该面的垂线，与二次曲面产生的交点，该点的法线和点的坐标被如下定义：
由于交点在二次曲面上，且两个坐标已知，则交点为

$\begin{align*} &\mathbf{p}_o=[\hat{o}_1,\hat{o}_2,s_3(\frac{\hat{o}_1^2}{s_1^2}+\frac{\hat{o}_2^2}{s_2^2})]^T \end{align*}$

所以在将该点带入曲线方程的三个偏导，得到此处切平面的方向向量

$\begin{align*} &f(\hat{x},\hat{y},\hat{z})=\frac{sign(s_1)}{s_1^2}\hat{x}^2+\frac{sign(s_2)}{s_2^2}\hat{y}^2-\frac{1}{s_3}\hat{z}=0\\ &\frac{df}{dx}=\frac{2sign(s_1)x}{s_1^2}\\ &\frac{df}{dy}=\frac{2sign(s_1)y}{s_y^2}\\ &\frac{df}{dz}=-\frac{1}{s_3}\\ &\hat{\mathbf{n}}(\mathbf{p}_o)=[\frac{2sign(s_1)\hat{o}_1}{s_1^2}, \frac{2sign(s_2)\hat{o}_2}{s_2^2}, -\frac{1}{s_3}]^T\\ \end{align*}$

点的法线不仅与二次曲面本身有关，也与摄像机的所处位置有关。

对于这个已知的点 $\mathbf{P}_o$ ，从摄像机到该点在法线 $\hat{\mathbf{n}}(\mathbf{p}_o)$ 的投影为 $m$ ，即

$m= \frac{\hat{\mathbf{n}}(\mathbf{p}_o)(\mathbf{p}_o-\hat{\mathbf{o}})}{||\hat{\mathbf{n}}(\mathbf{p}_o)||}$

而通过几何上的推导，得到直角三角形中的角 $\theta$ 的 $\cos$ 值，即

$cos\theta= \frac{\hat{\mathbf{r}}\cdot\hat{\mathbf{n}}(\mathbf{p}_o)}{||\hat{\mathbf{r}}\cdot||\hat{\mathbf{n}}(\mathbf{p}_o)||}$

所以通过除以 $\cos\theta$ 可以得到交点的深度，即

$\begin{align*} n&=\frac{m}{\cos\theta}=\frac{\hat{\mathbf{n}}(\mathbf{p}_o)\cdot(\mathbf{p}_o-\hat{\mathbf{o}})}{\hat{\mathbf{r}}\cdot \hat{\mathbf{n}}(\mathbf{p}_o)}\\ &=-\frac{C}{B}(\mathbf{A<1e-6}时成立) \end{align*}$

对于二次曲面本身具有二阶几何的性质，所以它也能够提供额外的性质，比如曲率，曲率的定义如下所示：

$\begin{align*} &\lambda_1=sign(s_1)s_3/s_1^2\\ &\lambda_2=sign(s_2)s_3/s_2^2\\ &\hat{K}_0(\hat{\mathbf{P}_0})= \frac{4\lambda_1\lambda_2}{(1+4\lambda_1^2\hat{x}_0^2+4\lambda_2^2\hat{y}_0^2)} \end{align*}$

对于渲染到图像的法向图和曲率图，作者使用了 alpha-blending，先对二次曲面体素单元进行排序，再进行渲染，即

$\begin{align*} N(u,v)=\sum\limits_{i=0}^{N-1}G_i\alpha_i\mathbf{n}_i\prod_{j=0}^{i}(1-G_j\alpha_j)\\ K(u,v)=\sum\limits_{i=0}^{N-1}G_i\alpha_iK_i\prod_{j=0}^{i}(1-G_j\alpha_j) \end{align*}$

7. 排序算法

对于 2DGS 等工作的方法，均是利用高斯中心深度，或说不透明度积累到一定阈值时的深度作为真实深度使用，但这会造成伪影等情况，诸如：

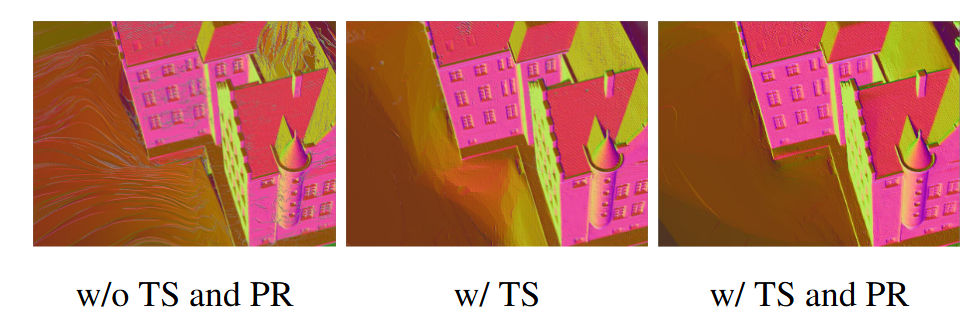
StopThePop排序算法

作者在本方法提出了两个排序过程，先后进行

Tile sort：在 3DGS 和 QGS 中，tile 的范围为 16*16，所以对于每个 tile 内的排序，找到一个离二次曲面中心投影到成像平面最近的光线，按这条光线求出的深度对二次曲面进行排序，tile 中 256 个像素均按这个排序。
Per-Pixel resort：对于 tile 内的像素，在 3DGS 中，渲染时顺序是一致的，只是每个高斯球对 tile 内的像素的影响不同。在 QGS 中，参考了 StopThePop 中的 per-pixel local resorting，具体做法为：
- 在求得每个高斯的深度、法线和曲率等其他性质时，对每个像素不直接开始 alpha-blending
- 在对每个像素进行 alpha-blending 时，在之前 tile sort 的基础上，重新用 像素中心-相机中心 的光线替代该像素所属的 tile 的 tile 中心-相机中心 ，并设置一个长度为 8 的滑动窗口，进行局部重排，能够提升渲染质量。
  8. 损失
  QGS 的损失参考了 2DGS 的深度损失和法线损失，其中深度损失旨在让高斯集中，并分布于表面；法线损失旨在在高斯的法线尽量与真实平面相符合。
  2DGS 中的法线损失使用了邻近点计算法线作为参考，但 2DGS 的平面属性决定了，其对变化剧烈的几何边缘无法进行处理，会产生伪影漂浮等问题。
  但 QGS 之前计算的曲率就可以用于改善这个问题，它使用曲率对法线进行指导，避免了变化剧烈的边缘处由于 “真实法线” 的不正确性，而导致的表面过于平滑和边缘处重建错误的问题，所以具体作用为：
曲率大的地方，降低法线损失的权重
曲率小的地方，提升发现损失的权重

所以总体损失为：

$\begin{align*} &L_d=\sum\limits_{i=0}^{N-1}\sum\limits_{j=0}^{i-1}\omega_i\omega_j(t_i-t_j)^2\\ &L_n=\sum\limits_i\omega_i(1-\mathbf{n_i}^T\mathbf{N})\\ &\lambda_K(K(u,v))=1-sigmoid(\ln|K(u,v)|+\epsilon)\\ &L_{Kn}(u,v)=\lambda_K(K(u,v))L_n(u,v)\\ &L=L_c+\lambda_dL_d+\lambda_nL_{Kn} \end{align*}$

9. forward. cu

renderCUDA 函数

创建像素到相机中心的光线

1
2
3

// create the direction
float2 ray = { (pixf.x - principal_x) / focal_x, (pixf.y - principal_y) / focal_y };
float3 ray_point = { ray.x , ray.y, 1.0 };

新增的共享变量

__shared__ float collected_view2gaussian[BLOCK_SIZE * 16];
__shared__ float3 collected_scales[BLOCK_SIZE];
__shared__ float4 collected_rscales_opacity[BLOCK_SIZE];
__shared__ int3 collected_scales_sign[BLOCK_SIZE];

1. 高斯中值不透明度（T=0.5）时的高斯球数目
  1
  uint32_t median_contributor = -1;

用于计算法线和曲率的变量

float A = 0;
float dist1 = {0};
float dist2 = {0};
float curv1 = {0};
float curv2 = {0};
float median_weight = {0};
float curvature_sum = 0.0f;

对新增变量的初始化

collected_rscales_opacity[block.thread_rank()] = rscales_opacity[coll_id];
collected_scales[block.thread_rank()] = scales[coll_id];
collected_scales_sign[block.thread_rank()] = scales_sign[coll_id];
for (int ii = 0; ii < 16; ii++)
	collected_view2gaussian[16 * block.thread_rank() + ii] = view2gaussian[coll_id * 16 + ii];

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。