All-to-key Attention for Arbitrary Style Transfer

0. TLDR

该工作将注意力机制应用到2D风格迁移，并通过观察前述方法中不稳定的风格迁移缺陷，提出了”点-块”和”块-块”的两种注意力机制，用于在粗/细粒度下实现了可接受复杂度下优秀的风格迁移结果

效果对比

1. overall architecture

作者在这里的总体结构仍然是

• 使用 VGG19 作为特征提取网络
• 将原图和风格图输入，并得到不同层级的特征（作者此处选取了 $l\in RELU{3_{1},4_{1},5_{1}}$）
• 对比两者
• 返回修改原图像的特征

这里的对比两者，作者使用了 A2K 模块，输入原图和风格图的特征，得到转换后的特征

然后使用了 Adaattn 中的思想，将 encoder 进行 mirror（❓），进而将特征改变为颜色，然后输出风格迁移之后的 RGB 图

2. what is all-to-all?

作者介绍了以前关于 AST（风格迁移）中注意力机制的使用，其形式如下：

• 输入形如 $(H, W, C)$ 的内容特征图 $F{c}$ 和风格特征图 $F{s}$
• 通过 normalization 操作和可学习的 conv layer，得到注意力机制中的 $Q,K,V$，即 $$Q=f(N(F_{c})), K=g(N(F_{s})), V=h(F_{c})$$
• 通过注意力机制得到 attention score，形状为 $(H\times W, H\times W)$，代表了内容特征图中每一个特征向量对于风格特征图中每一个特征向量的 相似分数。 $$AttN=softmax(Q\cdot K^{T})$$
• 通过这个相似分数作为权重，将风格特征图中所有特征向量进行权重求和，得到 风格迁移特征图。

该方法简单直接，但有两个问题

• 扭曲的风格结果和不稳定的结果
• 图像尺寸较大时，时间复杂度极高

3. distributed attention

作者为了缓解以上问题，设计了新的注意力机制模块，被称为 A2K (all-to-key)，简要概括来说，将内容特征图中某位置一个特征向量与风格特征图中 某块 的总体特征向量进行注意力查询，这种方式既降低了复杂度，又通过风格特征图设置块的模式，扩大了区域，提高了迁移的稳定性。

Pipeline

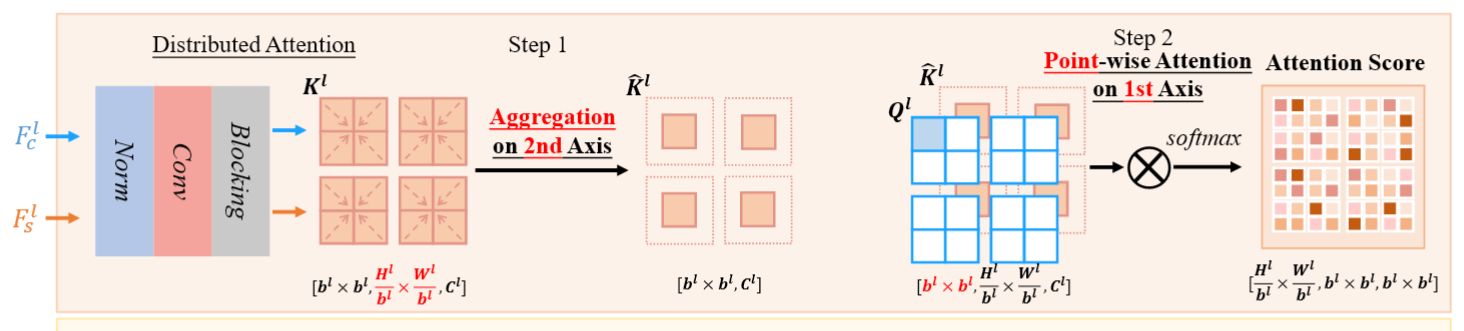
作者首先在可学习的 conv layer 后加入了一个类似 reshape 的操作：

reshape 过程中，我的理解如下：

• 将特征图分成块，其中包含 $\frac{H^{l}}{b^{l}}*\frac{H^{l}}{b^{l}}$ 个点。
• 将点按顺序排列好，作为 $Q^{l}$ 的第 2 维
• 分块按顺序排列好，作为 $Q^{l}$ 的第 1 维
• 每个点的特征都是 $C^{l}$ 维

内容特征图和风格特征图都完成以上的操作。

作者对风格特征图进行了 aggregation 的操作，概要来说就是将同一块内点的特征进行聚合，“合成为” 一个点，即：

其中 $k_i$ 为同一块内点的特征向量，该公式计算了该块内点的平均特征向量。

该公式则设置了一个可学习的线性变换 $\alpha, \beta$ ，并通过 sigmoid 将结果映射到 $[0,1]$ 内，最终计算出该块的 aggregation 的特征向量，由于共有 $b^{l}\times b^{l}$ 个块，aggregation 后得到的就是 $b^{l}\times b^{l}$ 形状的聚合特征矩阵 $\hat{K}^{l}$

此处之后，$Q^{l}$ 对应的就是内容特征图内单点的特征向量，而 $\hat{K}^{l}$ 对应的 aggregation 后以块为单位的特征向量，运用 all-to-all 的注意力机制，对第一维使用注意力（即原图的每个点和风格图的每块），就能得到新的 attention score 矩阵

• 第一维对应内容特征块中某一个点
• 第二维对应内容特征图中某一个特征块
• 第三维对应风格特征图中某一个特征块

4. Progressive Attention

对应上一节中 点对块 的注意力机制，这一节中使用了 块对块 的注意力机制获取索引，再使用 点对点 的注意力机制得到结果。

coarse
其中首先也使用了相同结构（但不是同一个）的 conv 和分块手法获取 $Q^{l}$ 和 $K^{l}$，为了获取内容特征图中某一块与风格特征图中哪一块最相近，作者使用了 argmax 的方法

$P^{l}_{1}$ 没有具体说明，我认为是 softmax 类似的操作，获取内容特征图中某一块与风格特征图中所有块的相似度，而 argmax 则是选取其中的最大值，并获取其序号，相等于获得了该块在风格特征图中相似度最大块的 序号。

fine
通过该方法重排风格特征图中每块的顺序，形成了相似度最高的一对一组合（块对块），并根据重排后的结果进行注意力机制的输出，对第二维使用注意力机制（即原图和风格图中特定块）

• 第一维：对应每一块
• 第二维：对应内容特征图中该块内的某一点
• 第三维：对应风格特征图中该块内的某一点
• 由于使用了 coarse 阶段的重排信息，fine 阶段的注意力机制只需要在很小一个区域（单个块）内进行，降低了时间复杂度并在近似度最高的块中进行风格迁移，提升了稳定度。

5. feature transformation

通过 distributed attention 和 progressive attention，能够对得到两种风格迁移项，与原特征累加，就能得到风格迁移后的结果

6. Complexity

通过分块能极大的降低 attention 环节的计算量，具体复杂度不写了（

7. Loss

首先是将风格迁移图输入 VGG 得到不同层的特征图，并计算每张特征图的 $\mu, \sigma$ ，并与风格图的特征图进行对比，这个类似于 AdaIN 吧

其次是使用 A2K 得到的迁移特征图作为 GT 进行对比